みなさん、こんにちは
チョークです
「0.57」って聞いて何を思い浮かべますか?
伴走沼にハマっていたら、「あぁ、葉っぱの面積ね」って思うんでしょうか?
うちの子は、3月頭くらいに「葉っぱの解き方」として、正方形内の弧のいわゆる葉っぱ問題について、先生から正方形の面積に「0.57」をかける方法を聞いてきたようで、家でも自慢をしていました
中学受験未経験の私は、そんな解き方は覚えてもいませんでした(円周率をπで表すとこのとき方はそもそも使えないですしね)
ただ、算数嫌いのうちの子にしては、0.57はしっかりと覚えていたので、私にとっても印象深い数字となりました
今日、次のような問題をやりました(斜線部の求積問題です)
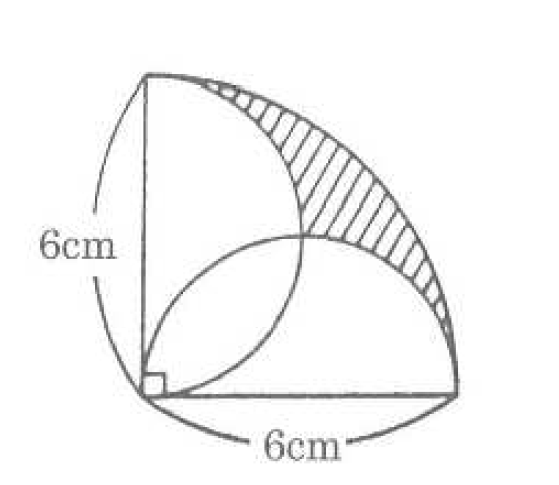
知っている人は知っているんでしょうが(ネットで調べたら当然知識として載っていました)、斜線部は、上記の図の一辺を3cmとした正方形内に構成される葉っぱと面積が同じとなります
というのも、半径6cm、中心角90度の扇形から、半径3cmの円一つ分を引き、そうすると引きすぎた扇形部分(重なるから2回引いた扱いとなる)を足して元に戻すところ、
6×6×π×90/360=3×3×π
となり、半径6cm、中心角90度の扇形から、半径3cmの円一つ分が面積が同じであるため、結果的に葉っぱ部分の面積を求めれば足りるということになるからです
うちでは、子度に問題をやらせている横で、私が先に解いて、子どもが分からなければ解き方を説明するという形で伴走をしているのですが、その前にやった葉っぱ問題は喜々として「0.57」を使って解いていた反面、この問題にはつまってしまっていたところ、「実は同じ面積だよ~」って話したところ、思いがけずテンションMAXに!
算数嫌いのイメージしかなかった我が子が、算数のことでこんなに喜ぶなんて!
とうれしくなったので、記事にしてしまいました


