皆さん、こんにちは
チョークです
今日は特殊算の代表格、つるかめ算の基本について話したいと思います

つるかめ算って、鶴と亀が出てくるんですか?

そうだよ
鶴と亀が出てくるんだ
鶴は足が2本、亀は足が4本ってことを前提として、「頭の数は全部で10だけど、足の数が全部で32本。さて、亀は何匹いますか?」っていう感じの問題が基本形になるんだよ

合計で10くらいなら、数えてしまえばいいじゃない!

10くらいなら、それもできないこともないかもね。凄く大変だと思うけど
でも、100とか1000でも数えるのかな?

そんなの数えられないわ
解き方を教えて欲しいな、チョーク

つるかめ算のポイントは、一方に寄せるところから考えることなんだよ
今回でいえば、亀の数を聞かれているから、最初、亀は0匹で全部鶴、つまり鶴が10羽いるって前提で考えるんだよ
下の図を見て気づくことはあるかな?
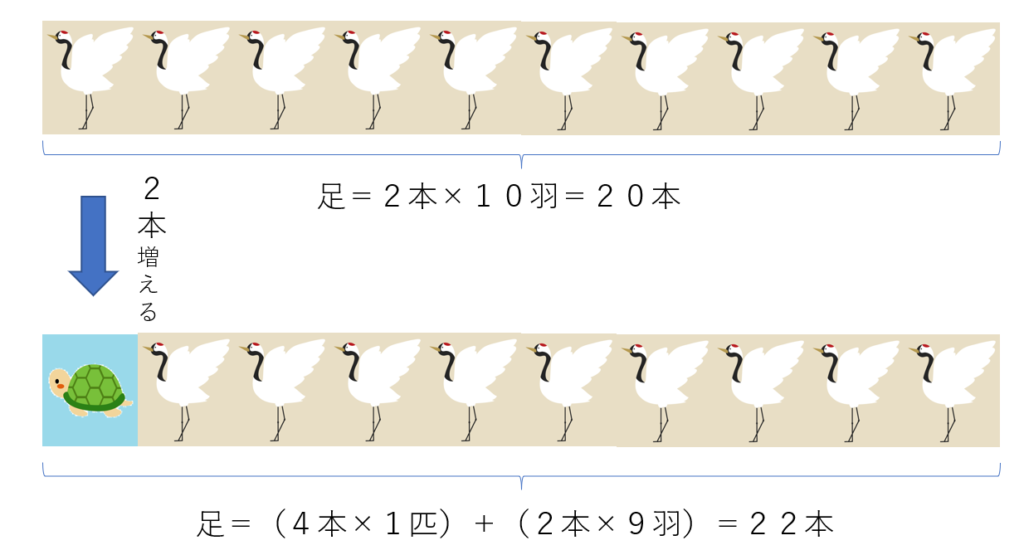

亀が0のとき、つまり、鶴が10羽のとき、足の合計は
2本×10羽=20本
となるけれど、亀1匹、鶴9羽のとき、足の合計は
亀の(4本×1匹)と鶴の(2本×9羽)の合計で22本になるよね
ここで注目して欲しいのは、亀が1匹増えると足の数が2本増えるってことなんだ

確かにそうね、、、

ここから分かることは、「鶴→亀」と1匹置き換えると、つまり、亀を1匹増やすと足が2本増えるっていうこと
最初の状態だと問題で要求されている32本に対し鶴だけだと20本しか足がなく
32本-20本=12本
で、12本足が不足しているよ
そうすると、亀に何匹置き換えたら問題の要求する足の本数になるかな?

1匹置き換えると2本足が増えるってことと、12本足が足りないってことだから
12÷2=6
で、6匹かな?

正解!
よくできたね
ここで気をつけて欲しいのは、答えで数を聞かれている亀を最初に0と設定することなんだ
逆に鶴を0羽、亀を10匹から計算しちゃうと、鶴の数が出てしまい、10から鶴の数を引かなければならなくなるから手間が増えるし、ケアレスミスを招く危険があるんだ
ちなみに、数式として表すと
亀の数=(問題で設定された足の本数-全部鶴の時の足の数)÷(亀と鶴の足の数の差)
={32本-(2本×10羽)}÷(4本ー2本)
って立式できるよ
以上、つるかめ算の基本的な考え方でした
つるかめ算については別解もありますが、今日は基本的な考え方です
自分なりにかみ砕いて説明をしてみましたが、いかがでしたでしょうか



